久々に算数問題です。
小五のムズイ算数ってことで。
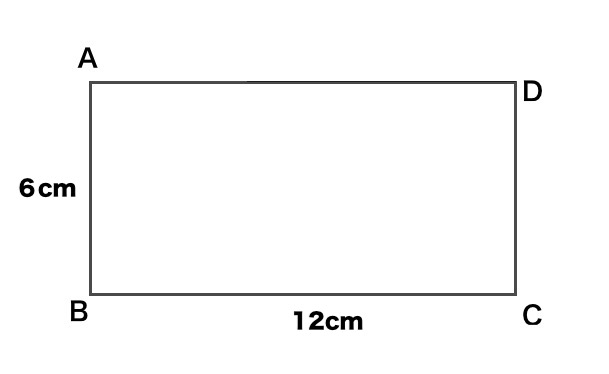
図1のような、たて6cm 横12cmの長方形ABCDがあります。この長方形を、図2のように、B とDが重なるように折ると、五角形EFGCDの面積が49.5㎠ になりました。このとき、次の問題に答えなさい。
(1)三角形DFGの面積を求めなさい。
(2)FDの長さを求めなさい。
(3)GDの長さを求めなさい。

本当は色を塗り塗りすると理解しやすいけど、いちおう「鉛筆のみ」とう条件でやってみましょう。
まずまず、、、(1)
もともとの長方形は72㎠ です。
五角形EFGCD(49.5㎠ )= 四角形EFGD+三角形DGC
折ったのだから四角形ABGFと四角形EFGDはまったくの同じ形で同じ面積です。
三角形DFG = 四角形ABCD(72㎠ )ー(四角形ABGF+三角形DGC)
三角形DFG = 四角形ABCD(72㎠ )ー(四角形EFGD+三角形DGC)
三角形DFG = 四角形ABCD(72㎠ )ー 五角形EFGCD(49.5㎠ )
三角形DFG = 72㎠ ー 49.5㎠ = 22.5㎠
なるほどね。
では(2)
三角形DGCの底辺はFDで高さ6cm で面積は22.5㎠
ほなら22.5 = FD×6÷2
計算してFD = 7.5cm
次に(3)
四角形ABGFと四角形EFGDはまったくの同じ形だから角FGB=角DGF
ADとBCは平行なので角FGB=角DFG
上の2つより角DGF=角DFG
従って、三角形DFGはDを頂点とする二等辺三角形
これよりFD=GD
だから同じく 7.5cm
よく出来たね〜