またしても算数問題で悩みます。
1/360 2/360 3/360 、、、、359/360 360/360 のうち約分できない分数はいくつありますか?
360逆割り算してみて
360=2☓2☓2☓3☓3☓5
従って、分子に2か3か5の倍数があると必ず約分できる。
だから「1から360までのうち、2か3か5で割り切れない数」を求めればイイジャン、楽勝楽勝。
2,3、5でそれぞれ割り切れる整数の数は
(ア)360÷2=180
(イ)360÷3=120
(ウ)360÷5=72
2と3,2と5、3と5の両方で割り切れる数がダブルでカウントされてるもんね
(エ)360÷6=60
(オ)360÷10=36
(カ)360÷15=24
そうそ、2と3と5の3つで割り切れる数はトリプルでカウントされてるじゃん
(キ)360÷30=12
(ア)+(イ)+(ウ)ー(エ)ー(オ)ー(カ) まではよいとして、、、(キ)はどうする?
(エ)と(オ)と(カ)で3回引いてるんだから2回足すんじゃあないだろうか??
ウエ〜、良くわかんない、、ORZ
よし、Excelでやってみよう!!!
A列には1〜360まで連続データを入れる
B列は2で割れたら1、割れなかったらスペース
C列は3で割れたら1、割れなかったらスペース
D列は5で割れたら1、割れなかったらスペース
E列1行目はB1+C1+D1として、それを360列までコピペ
F列1行目はIF関数で、Eが0だったらそこに1、Eが0じゃなかったらそこに0、、それを360列までコピペ
でF1からF360まで足し算してみるSUM(F1:F360)ですね。
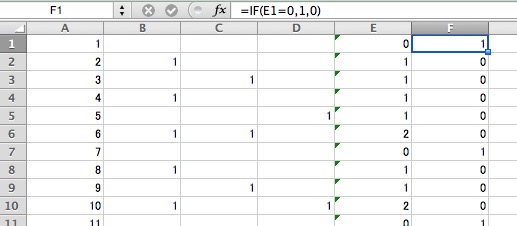
これで合ってるよな〜?

96ってことは、、、
つうことはだよ、、、360−96=264だから、、、
(ア)+(イ)+(ウ)ー(エ)ー(オ)ー(カ)=252
264−252−12
(キ)は1回だけしか足さないんだ、、、なんだか納得いかんな〜。
要は下の大きな四角に360個の数字が入っていて、A B C X Y Z Tを足した数を引けば良いんだろう?

(ア)360÷2=180 → A+X+Z+T
(イ)360÷3=120 → B+X+Y+T
(ウ)360÷5=72 → C+Y+Z+T
(エ)360÷6=60 → X+T
(オ)360÷10=36 → Z+T
(カ)360÷15=24 → Y+T
(キ)360÷30=12 → T
な、、な〜るほど、、
(ア)+(イ)+(ウ)ー(エ)ー(オ)ー(カ)=A+B+C+X+Y+Z になるから T が消えちゃうのね。
とココまで書いて(ア)(イ)(ウ)で T の部分を3回カウントしたのに、(エ)(オ)(カ)で3つとも削除しちゃってるもんね、、と気がつくのでした。気がつくの遅いし。