算数問題で忘れがちなところなのでメモです。
問題:1辺1cmの立方体を図のように並べ対角線となるAGを通る線で串刺しにしました。
串刺しにされていない立方体の体積は?
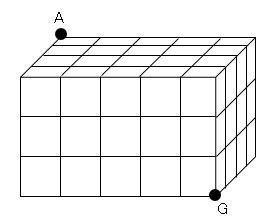
まず、、5×4×3=60 だから60個以下だな。えーーと何だっけ?
えーーっと、左上はまず串刺しされ、次は、、、ん?
公式ってあったっけ?わすれた、、完全に躓きます。
まず、平面の問題を考えてみます。
問題:正方形のタイルを図のようにきっちりとならべ、対角線でズバッと切り、2つの三角形に分かれます。
そのとき、1つの三角形に「無傷の正方形」はいくつありますか?
んまあ、このぐらいならフリーハンドで綺麗な図形を描けたら数えるだけ。
答えは4つです。


でも数が多かったら、図形を描いて数える気が起きますか?(縦71、横37とかw)
この問題は、無傷の数を数えるのではなく、何枚が切られているかを考えます。
「縦の数」+「横の数」ー1=切られた数
という公式を知っていれば、切られた数=5+3ー1=7とわかるので
無傷のタイルは、3×15−7=8
三角形は2つあるので、8÷2=4 答え 4つ
となります。

「縦の数」+「横の数」ー1=切られた数
を忘れていなければ良いのですが、忘れちゃった時の考え方。
まず右上(または左下でもヨシ)の□は必ず切られます。
そして切った線は縦方向、または横方向の辺1つを通過して、お隣に移動していきます。
移動する時に通過する辺は下図のように、縦方向に4カ所、横方向に2カ所であることがわかります。
縦なら、5つ並べたタイルの間なので5−1です。
横なら、3つ並べたタイルの間なので3ー1です。
「切られた数」=「最初の1」+「縦の数−1」+「横の数−1」=「縦の数」+「横の数」ー1

しかしながら、これは「格子点」を通らないという条件の元のみです。
タイルが縦に12枚、横に9枚なら、
12:9=4:3
12÷3=4
9÷3=3
ですので、縦4枚、横3枚というのが3ブロックあると感がえます。
赤で括ったひとつのブロックで
4+3−1=6
3ブロックあるので
6×3=18
ですので、切られているタイルは18枚
切られていないタイルは12×9ー18=108−18=90
切られていないタイルは全部で90枚
もし、三角形1つの数を聞かれたのなら45枚ですね。

ということで、最初の問題に戻ります。
立体ですので、A – Gを通過する線は今通過したサイコロの1つの面から次の面を刺すことになります。
(辺ではなく面ですが、串刺しの線が1度に他の2面を同時に通過することはあり得ません)
また並んでいるサイコロの数は3、4、5 ですから(最大公約数が1ですから)、串刺しの線は必ず次の面を通過します。
従って、Aから串刺ししていった場合、次のサイコロの必ず(下か、手前か、横か)の1面を串刺しにしながら突き進むことになります。
ということで、
まずは、最初のAがあるサイコロを串刺しし、、
下方向には「3つー1」
右方向には「5つー1」
手前方向に「4つー1」
つの面を通過することとなります。
従って、合計:1+(3−1)+(5−1)+(4−1)=10
10個のサイコロを串刺しにしてます。
ということで、串刺しにされていないサイコロは60−10=50
1つ1立方センチメートルなので、答えは50立方センチメートル
平面の場合
X+Y−1 とは覚えず
1+( X−1)+( Y−1)
立方体の場合
X+Y+Z − 2 とは覚えず
1+( X−1)+( Y−1)+( Z−1)
と何度か図形を描きながら覚えたほうが良いでしょうね。
ということで、サイコロが縦4こ、横6こ、奥に5こなら複雑です。
縦2こ、横3こ、奥に5 のブロックを2つと考えます。
1+( 2−1)+( 3−1)+( 5−1)=8
これが2つあるので、8×2=16
全体が4×6×5=120個あるので、120ー16=104
答えは104立方センチメートル
もうココまで来ると「感性」がないとダメかも。