それほど本業が忙しくない予定だったのに忙しい1日でした。
さて、月曜日の続きなんですが、立方体を貫く線が面ではなく辺を貫く時も同じく考えていいんだよなー
そうだよ、辺でも面でも次に来る立方体に、、、あれ?じゃあ、貫かれた立方体の表面積って言われたらどうなるんだ?
?? と考えながら夕食です。
夕食は、余り物でパスタ2種類とほうれん草のおつまみ。

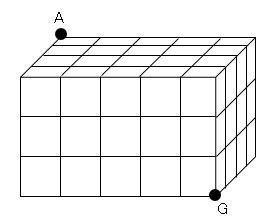
串刺しされた立方体は、下手くそな四角い団子のような感じで繋がってます。
この立方体の面積を聞かれたら、、
串刺しされた立方体の数は
1+(3−1)+(5−1)+(4−1)=10
10個の立方体が繋がっている。
1面は1㎠ で、立方体なので1つの立方体の表面積は 6㎠
これが10あるので、もしバラバラなら60㎠
んで、面と面が接しているところが9箇所ある。
っていうことは18面は隠れるから60ー18=42㎠
これでメデタシメデタシ、、だ。
立方体が縦4こ、横6こ、奥に5こなら
縦2こ、横3こ、奥に5 のブロックを2つと考えます。
1+( 2−1)+( 3−1)+( 5−1)=8
1面は1㎠ × 6= 6㎠ これが8あるので、もしバラバラなら48㎠
んで、面と面が接しているところが7箇所ある。
っていうことは14面は隠れるから48ー14=34㎠
これが2ブロック分だから
34㎠ × 2=68㎠
たぶん、コレであっていると思う
でも、、縦30 横45 奥18だったらどうすんだべ? と深追いしてみる。
最大公約数はなの3で、縦10 横15 奥6 の場合×3と考えてよし。
串刺しにされている立方体は1ブロック
1+(10−1)+(15−1)+(6−1)=20
だから20×3=60個
ここまではいいはずだ。
んで、、、隠れてる面は、、、んと、、縦10と横15って5で割るから、、そのときは面じゃなくて辺通過で
わからん。と悩み中。