いわゆる「ベンツ切り」の考え方の基本です。
あのスリーポイントマークと何となく図形が似ていることから由来されていると思います、扇の問題はレクサス角度と言いますから(ウソ)。
はいはい、下の図を見て頭が痛くなっちゃったそこの貴方はスルーしてください。
普通に生きていく上で、何の必要性もありませんから(笑
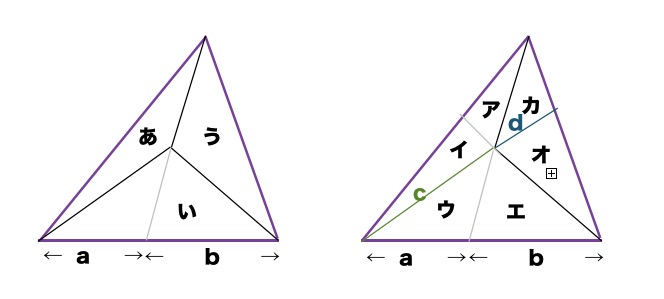
左図
a の長さ:b の長さ = あの面積:うの面積
右図
c の長さ:d の長さ = ア+イの面積:カの面積 = ウ+エの面積:オの面積
まあ知っておくとイロイロ便利。
だけど
「こういう法則なんだ!!何でも良いから覚えちまえ!!」
より
「ここがこうで、こうなって、、、ほらね」
と説明したかったのですが、ネットの説明があまりにも分かりにくかったのでした。
以下の説明は、基本的な三角形の面積が “ひねくれた三角形” でも計算できたらそれで出来ます。

一応、、、上の図で三角形AもBもCもDも底辺の長さが同じで、上下の実線が平行だと思ってください。
三角形の面積は(底辺×高さ)÷2ですから、上の4つの三角形は底辺と高さが同じです。
従って、三角形の面積はA=B=C=D です。
これはOK ですね!
また、底辺が2倍になれば面積も2倍、1/2なら1/2になるってこともOKですね?
では、、

まず、左図に赤の補助線(三角形の下の辺と平行)を引きましょう。
あをあ1とあ2に、うをう1とう2に分けました。
赤線の左側と右側の比はa : bの長さの比と同じになりますね。
a : b = a’ : b’
あ1とう1は高さ(h1)が一緒です。従って、あ1:う1 = a’ : b’ = a :b
あ2とう2は高さ(h2)が一緒です。従って、あ2:う2 = a’ : b’ = a :b
従って、a の長さ:b の長さ = あの面積:うの面積
じゃあ、次に右の図ね、、cdから延長した補助線を書きましょう。そしてそれに平行で上の頂点を通過する補助線も書きましょう。すると高さ(h3)が見えてきましょう。従って、高さが一緒ですので、ア+イ:カ= c:d ってことです。
ということで、本業後に他医院に行きましてちょいと仕事をしました。
(あ、歯科医業じゃあないですよ〜♪)




















